TPU MatMul Kernel 矩阵乘法算子

11月 27, 2024·
田山泉
田山泉
· 2 分钟阅读时长

矩阵乘法（MatMul）是机器学习的核心运算。对矩阵乘法进行高效实现，对于充分利用Google TPU等硬件加速器尤为重要。JAX的Pallas框架允许开发者为TPU编写低级别的、高度优化的Kernel。在本文中，我将分享我使用JAX Pallas实现MatMul Kernel的初步探索，展示不同优化策略如何影响TPU性能。

Why Optimize MatMul for TPUs?

与GPU不同，TPU采用的是专为机器学习设计的SIMD脉动阵列（Systolic Array）架构。然而，想要实现最佳性能，需要精细地考虑内存使用、并行化策略和数据精度。

下面我们将深入不同实现方式，并总结各自的效果和启示。

Kernel Implementations Explored

1. Naive MatMul

最基础的Kernel一次性将整个矩阵加载到TPU的向量内存（VMEM）中：

def matmul_v1_kernel(a_ref, b_ref, o_ref):
  o_ref[...] = a_ref[...] @ b_ref[...]

在该实现中，输入矩阵 [M, K] 和 [K, N] 完全加载到VMEM，输出矩阵 [M, N] 也存储在VMEM。尽管简单，但当矩阵尺寸超过1024时，内存迅速耗尽。下图显示只能处理 M=K=N ≤ 1024的尺寸。当尝试 [2048, 2048] 时，会发生“内存耗尽”的错误.

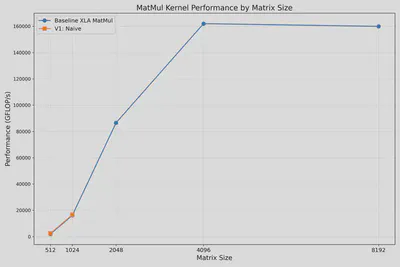
Kernel 1 Performance

2. Parallel MatMul

将矩阵拆分成更小的块可以降低VMEM使用量：

def matmul_v2_parallel_kernel(a_ref, b_ref, o_ref):
  o_ref[...] = a_ref[...] @ b_ref[...]

@functools.partial(jax.jit, static_argnames=['N'])
def run_matmul_v2(a: jax.Array, b: jax.Array, N: int):
  kernel = pl.pallas_call(
      matmul_v2_parallel_kernel,
      grid=(N, N),
      in_specs=[
          pl.BlockSpec((a.shape[0] // N, a.shape[1]), lambda i, j: (i, 0)),
          pl.BlockSpec((b.shape[0], b.shape[1] // N), lambda i, j: (0, j)),
      ],
      out_specs=pl.BlockSpec(
        (a.shape[0] // N, b.shape[1] // N), lambda i, j: (i, j)),
      out_shape=jax.ShapeDtypeStruct((a.shape[0], b.shape[1]), a.dtype)
  )
  return kernel(a, b)

该Kernel将矩阵A按行、矩阵B按列切分。虽然稍微降低了内存消耗，但获得的并行性能仍然低于XLA内置的jnp.matmul()函数。下图显示了N=4的并行结果，可处理最大尺寸提升到2048，但性能仍不及XLA库：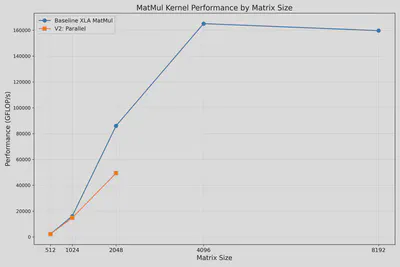

Kernel 2 Performance

3. Block-Based MatMul (3D Grid)

采用3D网格分块的方法进一步优化内存管理。此前，将整个 [block, M] 或 [M, block] 矩阵加载到VMEM占用仍较大。我们可以定义一个3D网格[bm, bk, bn]，更细粒度地切分输入输出矩阵，并在每个K迭代中初始化输出：

def matmul_v3_block_kernel(a_ref, b_ref, o_ref):
  @pl.when(pl.program_id(2) == 0)
  def init():
    o_ref[...] = jnp.zeros_like(o_ref)
  # 累加每个block的乘法结果
  o_ref[...] += a_ref[...] @ b_ref[...]


@functools.partial(jax.jit, static_argnames=['bm', 'bk', 'bn'])
def run_matmul_v3(
    a: jax.Array,
    b: jax.Array,
    *,
    bm: int = 128,
    bk: int = 128,
        bn: int = 128):

  m, k = a.shape
  _, n = b.shape
  assert k == b.shape[0]

  run_kernel = pl.pallas_call(
      matmul_v3_block_kernel,
      grid=(m // bm, n // bn, k // bk),
      in_specs=[
          pl.BlockSpec((bm, bk), lambda i, j, k: (i, k)),
          pl.BlockSpec((bk, bn), lambda i, j, k: (k, j)),
      ],
      out_specs=pl.BlockSpec((bm, bn), lambda i, j, k: (i, j)),
      out_shape=jax.ShapeDtypeStruct((m, n), a.dtype),
  )
  return run_kernel(a, b)

此实现显著降低了内存占用，可以处理更大矩阵，但性能依然落后于XLA优化库。下图显示所有尺寸均可成功计算，但性能较差：

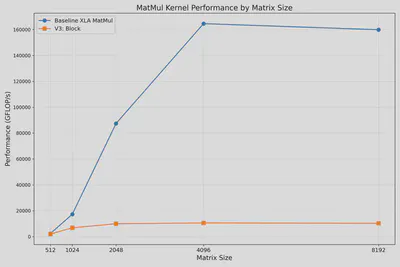
Kernel 3 Performance

4. Optimal Block Size Strategy

与GPU不同，TPU并非基于线程并行执行，而是SIMD脉动阵列，单个Kernel表现为顺序执行模式。因此，通过搜索最佳block尺寸（bm, bk, bn）可以达到更优性能：

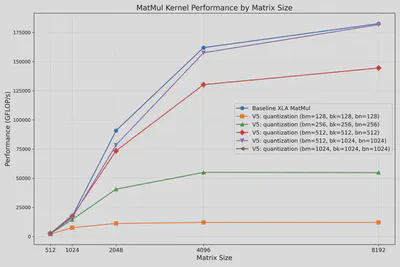
下图展示了寻找最佳尺寸的过程。实验表明（bm, bk, bn）=（512, 512, 512）下取得了最佳FLOP/s性能。

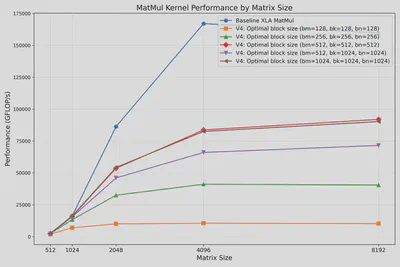
Kernel 4 Performance

5. Precision Optimization: Quantization

最优的分块尺寸会随精度的变化而改变。以下是采用BFLOAT16精度时的最佳性能表现。（bm, bk, bn）=（512, 1024, 1024）几乎达到XLA库jnp.matmul()的性能：

Kernel 5 Performance

Key Insights

  • 内存管理：有效的内存拆分与分块是实现TPU高效并行的关键。
  • 分块尺寸：选择最佳分块尺寸能极大影响性能，需要实验进行调优。
  • 精度重要性：使用更低精度（如BFLOAT16）能提升性能及内存效率，特别是在更大规模时。

通过此次基于JAX Pallas框架的探索，我们获得了针对TPU优化的宝贵经验。定制Kernel使开发者能进一步挖掘硬件潜力，实现机器学习工作负载的显著性能提升。

欢迎访问repository ，以复现实验并进一步探索！

Acknowledgements

This project is inspired by JAX’s Pallas framework and builds upon the TPU programming model.

TPU Kernel MatMul